Inilah Pengertian, Ciri-Ciri dan Rumus Luas Kerucut yang Harus Diketahui

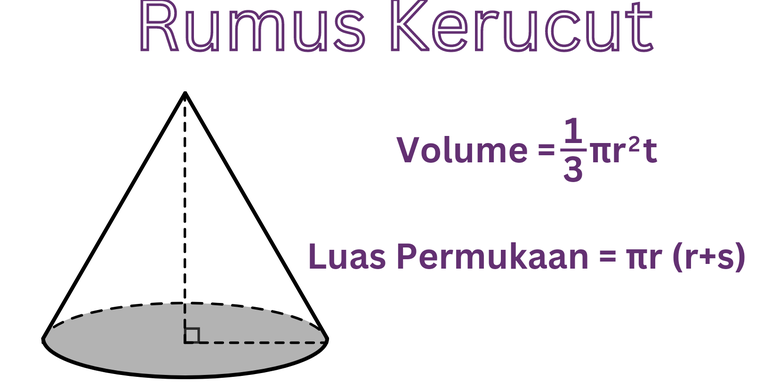
Rumus luas kerucut merupakan salah satu bagian dari materi geometri pada pelajaran matematika. Kerucut merupakan salah satu bangun ruang tiga dimensi dengan sisi lengkung seperti tabung dan bola.

Cone atau yang dikenal dengan kerucut ini masuk ke dalam golongan limas istimewa dengan alas yang berbentuk lingkaran. Nah, untuk bisa mengetahui lebih banyak mengenai kerucut, simak pengertian, ciri-ciri, dan rumus luas kerucut berikut ini.

• Apa itu Kerucut?

Kerucut merupakan bandung ruas tiga dimensi yang mempunyai satu alas berbentuk lingkaran dan memiliki sisi berupa bidang lengkung. kerucut memiliki beberapa unsur pembentuk yaitu tinggi, jari-jari, dan garis pelukis. Tinggi kerucut adalah jarak antara titik puncak dengan titik pusat alas.

Jari-jari kerucut merupakan jarak antara titik pusat alas dengan keliling lingkaran alas. Dan untuk garis pelukis merupakan garis penghubung puncak kerucut dengan keliling lingkaran alas.

• Ciri-ciri Kerucut

1. Memilik bentuk segitiga siku-siku atau segitiga sama kaki pada ketampakan dua dimensi.
2. Memiliki ketampakan dua buah garis yang tegak sebagai garis pelukis dan garis semu.
3. Memiliki satu buah rusuk yang keliling alasnya berbentuk lingkaran.
4. Memiliki dua buah sisi, lingkaran pada alas dan juring pada selimut.
5. Memiliki satu titik sudut yang berfungsi untuk puncak kerucut.

• Rumus Luas Kerucut

Seperti yang diketahui bersama bahwa kerucut memiliki permukaan yang terdiri atas semilut dan alas. Bentuk dari selimut kerucut memiliki juring lingkaran dengan alas yang berbentuk lingkaran sempurna.

Dengan begitu, permukaan kerucut merupakan hasil dari penjumlahan luas selimut di tambah dengan luas alas kerucut. berikut rumus yang bisa digunakan:

1. Rumus selimut kerucut: L = π r s.
2. Rumus luas alas kerucut: L = π R².
3. Rumus Luas Permukaan Kerucut: L = (π r s) + (π r²) atau L = π r (s+r).
4. Rumus menghitung garis pelukis: S = √r² + t².

Keterangan:

L = Luas permukaan kerucut.

r = Jari-jari.

π = 22/7 atau 3,14.

s = Garis pelukis.

t = Tinggi kerucut.

• Contoh Soal Luas Kerucut

Jika merasa bingung dengan penjelasan rumus di atas, simak beberapa contoh soal yang bisa membantu untuk memahami rumus tersebut.

1. Terdapat sebuah kerucut berdiameter 12 cm dengan tinggi 8 cm dan π = 3,14. Maka berapakah luas permukaan kerucut tersebut?

Diketahui d = 12 cm, r = ½ x d = 6 cm, t = 8 cm, π = 3,14. Jika ditanya berapa luas permukaan kerucut maka langkah pertama yang harus dicari adalah panjang garis pelukis seperti:

s = √r² + t²

s = √6² + 8²

s = √36 + 64

s = √100

s = 10. Lanjut dengan menghitung luas pemukaan kerucut.

L = π r (s + r)

L = 3,14 x 6 (10 + 6)

L = 18,84 x 16

L = 301,44 cm². Jadi luas permukaan kerucut di atas adalah 301,44 cm².

2. Terdapat sebuah bangun ruang kerucut yang memilik luas selimut 352,25 cm², panjang jari-jari 7,5 cm. Maka hitunglah luas permukaan kerucut tersebut.

Diketahui Luas selimut = 353,25 cm² dan r = 7,5 cm.

L = luas selimut + luas alas

L = (π r s) + (π r²)

L = (353,25) + (3,14 x 7,5 x 7,5)

L = 353,25 + 176,625

L = 529,875 cm². Jadi, luas permukaan kerucut adalah 529,875 cm².